RESEARCH: black holes

gravitational singularity

A gravitational singularity or space-time singularity is a location in space-time where the gravitational field of a celestial body becomes infinite in a way that does not depend on the coordinate system. The quantities used to measure gravitational field strength are the scalar invariant curvatures of space-time, which includes a measure of the density of matter. Since such quantities become infinite within the singularity, the laws of normal space-time could not exist. A type of singularity predicted by general relativity is inside a black hole: any star collapsing beyond a certain point (the Schwarzschild radius) would form a black hole, inside which a singularity (covered by an event horizon) would be formed.The Penrose–Hawking singularity theorems define a singularity to have geodesics that cannot be extended in a smooth manner. The termination of such a geodesic is considered to be the singularity. According to modern general relativity, the initial state of the universe, at the beginning of the Big Bang, was a singularity. Both general relativity and quantum mechanics break down in describing the earliest moments of the Big Bang, but in general, quantum mechanics does not permit particles to inhabit a space smaller than their wavelengths.

Types

There are different types of singularities, each with different physical features which have characteristics relevant to the theories in which they originally emerged from, such as the different shape of the singularities, conical and curved. They have also been hypothesized to occur without Event Horizons, structures which delineate, one space-time section from another in which events cannot affect past the horizon, these are called naked.

cone: space-time looks like a cone around this point, where the singularity is located at the tip of the cone.

curvature:e. In coordinate systems convenient for working in regions far away from the black hole, a part of the metric becomes infinite at the event horizon. However, space-time at the event horizon is regular.

More generally, a space-time is considered singular if it is geodesically incomplete meaning that there are freely-falling particles whose motion cannot be determined beyond a finite time, being after the point of reaching the singularity. For example, any observer inside the event horizon of a non-rotating black hole would fall into its center within a finite period of time. The classical version of the big bang cosmological model of the universe contains a causal singularity at the start of time (t=0), where all time-like geodesics have no extensions into the past. Extrapolating backward to this hypothetical time 0 results in a universe with all spatial dimensions of size zero, infinite density, infinite temperature, and infinite space-time curvature.

geodesics in space time

In general relativity, a geodesic generalizes the notion of a “straight line” to curved space time. Importantly, the world line of a particle free from all external, non-gravitational force, is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.

In general relativity, gravity can be regarded as not a force but a consequence of a curved spacetime geometry where the source of curvature is the stress energy tensor (representing matter, for instance). Thus, for example, the path of a planet orbiting around a star is the projection of a geodesic of the curved 4-D spacetime geometry around the star onto 3-D space.

black holes

A black hole is a region of space time exhibiting such strong gravitational  effects that nothing—not even particles and electromagnetic radiation such as light—can escape from inside it. The theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole. The boundary of the region from which no escape is possible is called the event horizon. Although the event horizon has an enormous effect on the fate and circumstances of an object crossing it, no locally detectable features appear to be observed. In many ways a black hole acts like an ideal black body as it reflects no light. Moreover, quantum theory in general space time predicts that event horizons emit hawking radiation, with the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is on the order of billionths of a kelvin for black holes of stellar mass making it essentially impossible to observe.

Black holes of stellar mass are expected to form when very massive stars collapse at the end of their life cycle. After a black hole has formed, it can continue to grow by absorbing mass from its surroundings. By absorbing other stars and merging with other black holes, supermassive blackholes of millions of solar masses may form. There is general consensus that supermassive black holes exist in the centers of most galaxies.

if a star is denser than GM/C² R≥1 then we see that no photon can ever leave the star since to do so requires more energy than its energy “hv”. the redshift would in effect, have then stretched the photons wavelength to infinity. a star of this type cannot radiate so would be invisible- A BLACK HOLE IN  SPACE.

schwarzschild radius

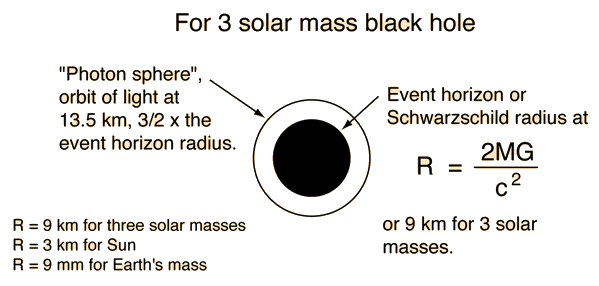
R_s=2GM/c²

the body is a black hole if all its mass is within the size of this radius. the boundary of a blackhole is called an event horizon. the escape speed form the black hole is equal to the speed of light c at the schwarzschild radius, hence nothing at at all can ever leave a black hole. for the stars having sun’s mass, R_s is 3km, a quarter of a million times smaller than the sun’s present radius. A black hole that is the member of a double star system will reveal its presence by its gravitational pull on the other star; the two star circle each other. In addition, the intense gravitational field of the black hole will attract matter from the other star, which will be compressed and heated to such high temperatures that x-rays will be emitted profusely. One of a number of invisible objects that astronomers believe on this basis to be black holes is known as cygnus-X1. The region around black hole that emits x-rays should extend outwards for several hundred kilometers.

The no hair theorem states that, once it achieves a stable condition after formation, a black hole has only three independent physical properties:Mass, charge and angular momentum .Any two black holes that share the same values for these properties, or parameters, are indistinguishable according to classical (i.e. non-quantum) mechanics.

These properties are special because they are visible from outside a black hole. For example, a charged black hole repels other like charges just like any other charged object. Similarly, the total mass inside a sphere containing a black hole can be found by using the gravitational analog of gauss law, the ADM mass, far away from the black hole.Likewise, the angular momentum can be measured from far away using frame dragging by the Gravitomagnetic field.When an object falls into a black hole, any information about the shape of the object or distribution of charge on it is evenly distributed along the horizon of the black hole, and is lost to outside observers. The behavior of the horizon in this situation is a dissipative system that is closely analogous to that of a conductive stretchy membrane with friction and electrical resistence- the membrane paradigm. This is different from other field such as electromagnetism, which do not have any friction or resistivity at the microscopic level, because they are time reversable. Because a black hole eventually achieves a stable state with only three parameters, there is no way to avoid losing information about the initial conditions: the gravitational and electric fields of a black hole give very little information about what went in. The information that is lost includes every quantity that cannot be measured far away from the black hole horizon, including approximately conserved quantum numbers such as the totalbaryon numbers and lepton number. This behavior is so puzzling that it has been called the black hole information loss paradox.